Skip to contents

Visualize effects and interactions

Source: vignettes/estimate_relation.Rmd
estimate_relation.Rmd

This vignette will present how to visualize the effects and interactions using estimate_relation().

Note that the statistically correct name of estimate_relation is estimate_expectation (which can be used as an alias), as it refers to expected predictions (read more).

Simple regression

Linear relationship 

library(modelbased)

model <- lm(Sepal.Length ~ Sepal.Width, data = iris)

visualization_data <- estimate_relation(model)
head(visualization_data)
> Model-based Predictions
> 
> Sepal.Width | Predicted |   SE |       95% CI
> ---------------------------------------------
> 2.00        |      6.08 | 0.18 | [5.73, 6.43]
> 2.27        |      6.02 | 0.14 | [5.74, 6.30]
> 2.53        |      5.96 | 0.11 | [5.75, 6.17]
> 2.80        |      5.90 | 0.08 | [5.75, 6.06]
> 3.07        |      5.84 | 0.07 | [5.71, 5.97]
> 3.33        |      5.78 | 0.08 | [5.62, 5.94]
> 
> Variable predicted: Sepal.Length
> Predictors modulated: Sepal.Width
library(ggplot2)
plot(visualization_data, line = list(color = "red")) +
  theme_minimal()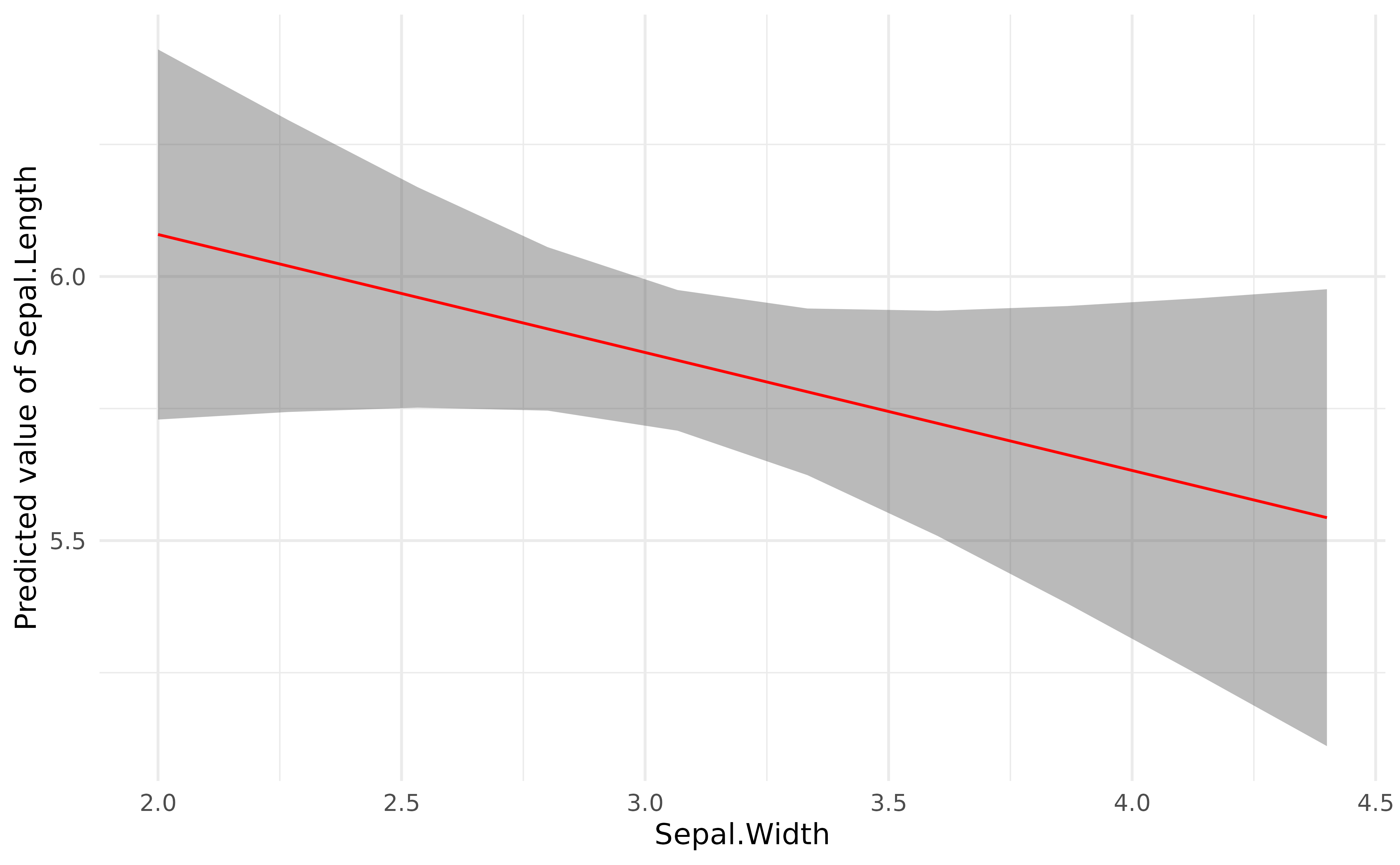

More complex regressions

Polynomial 

lm(Sepal.Length ~ poly(Sepal.Width, 2), data = iris) |>
  modelbased::estimate_relation(length = 50) |>
  plot()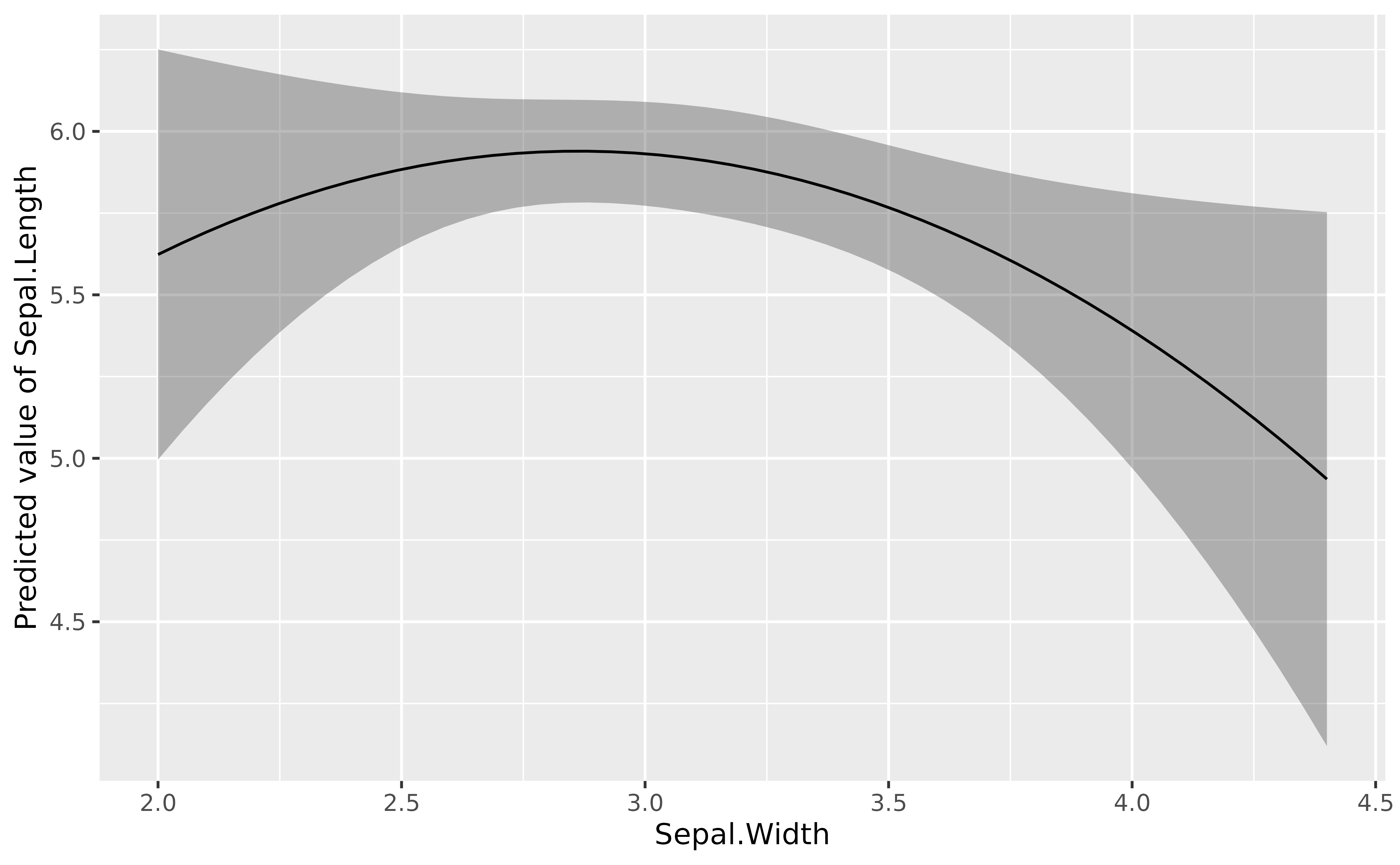

Additive Models 

library(mgcv)
> Loading required package: nlme
> This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
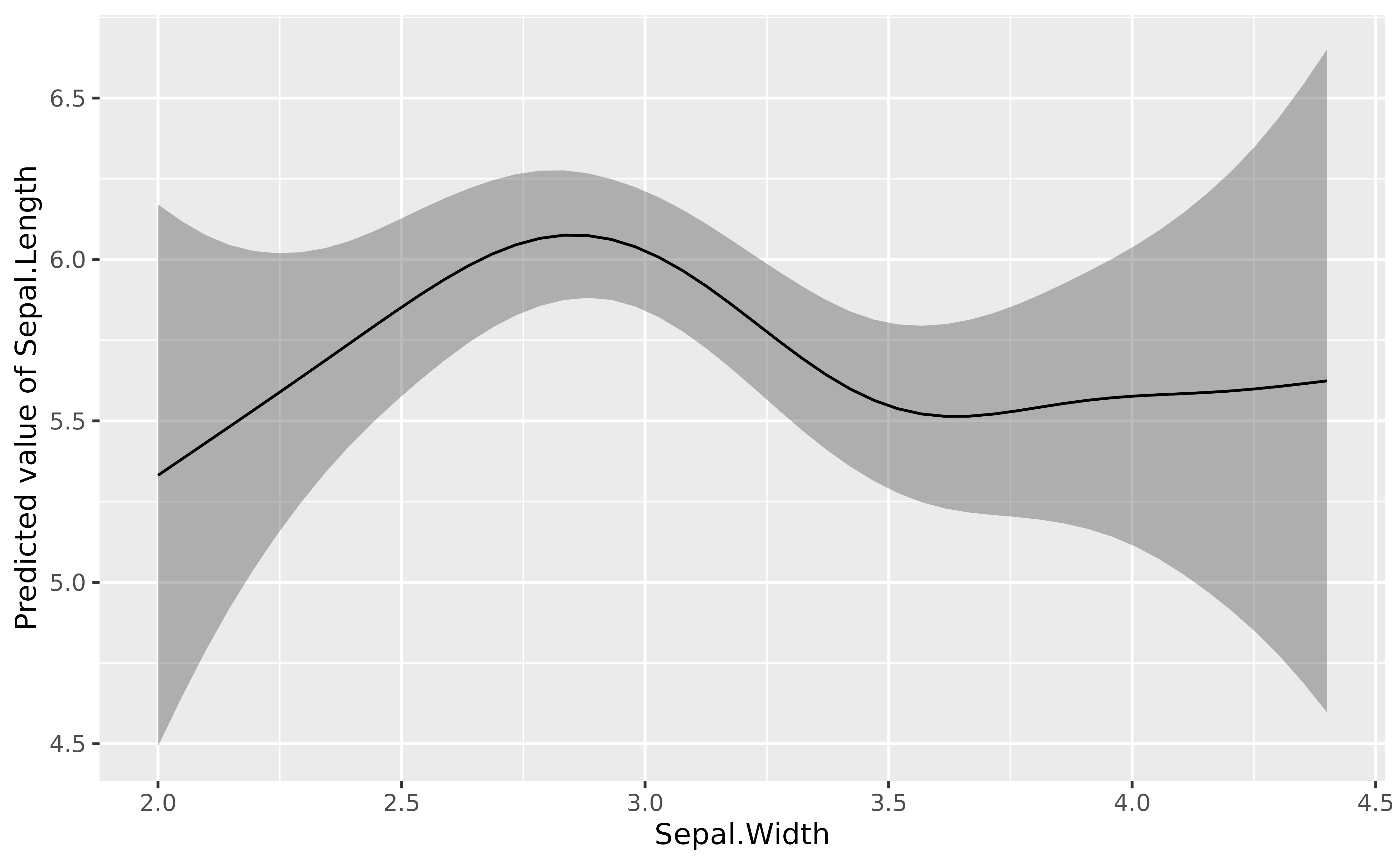
mgcv::gam(Sepal.Length ~ s(Sepal.Width), data = iris) |>
  modelbased::estimate_relation(length = 50) |>
  plot()

References