Compute the Probability of Direction (pd, also known as the Maximum Probability of Effect - MPE). This can be interpreted as the probability that a parameter (described by its full confidence, or "compatibility" interval) is strictly positive or negative (whichever is the most probable). Although differently expressed, this index is fairly similar (i.e., is strongly correlated) to the frequentist p-value (see 'Details').
Usage
# S3 method for class 'lm'
p_direction(
x,
ci = 0.95,
method = "direct",
null = 0,
vcov = NULL,
vcov_args = NULL,
...
)Arguments
- x
A statistical model.
- ci
Confidence Interval (CI) level. Default to
0.95(95%).- method
Can be
"direct"or one of methods ofestimate_density(), such as"kernel","logspline"or"KernSmooth". See details.- null
The value considered as a "null" effect. Traditionally 0, but could also be 1 in the case of ratios of change (OR, IRR, ...).
- vcov
Variance-covariance matrix used to compute uncertainty estimates (e.g., for robust standard errors). This argument accepts a covariance matrix, a function which returns a covariance matrix, or a string which identifies the function to be used to compute the covariance matrix.
A covariance matrix
A function which returns a covariance matrix (e.g.,
stats::vcov())A string which indicates the kind of uncertainty estimates to return.
Heteroskedasticity-consistent:
"HC","HC0","HC1","HC2","HC3","HC4","HC4m","HC5". See?sandwich::vcovHCCluster-robust:
"CR","CR0","CR1","CR1p","CR1S","CR2","CR3". See?clubSandwich::vcovCRBootstrap:
"BS","xy","residual","wild","mammen","fractional","jackknife","norm","webb". See?sandwich::vcovBSOther
sandwichpackage functions:"HAC","PC","CL","OPG","PL".
- vcov_args
List of arguments to be passed to the function identified by the
vcovargument. This function is typically supplied by the sandwich or clubSandwich packages. Please refer to their documentation (e.g.,?sandwich::vcovHAC) to see the list of available arguments. If no estimation type (argumenttype) is given, the default type for"HC"equals the default from the sandwich package; for type"CR", the default is set to"CR3".- ...
Arguments passed to other methods, e.g.
ci(). Arguments likevcovorvcov_argscan be used to compute confidence intervals using a specific variance-covariance matrix for the standard errors.
What is the pd?
The Probability of Direction (pd) is an index of effect existence, representing the certainty with which an effect goes in a particular direction (i.e., is positive or negative / has a sign), typically ranging from 0.5 to 1 (but see next section for cases where it can range between 0 and 1). Beyond its simplicity of interpretation, understanding and computation, this index also presents other interesting properties:
Like other posterior-based indices, pd is solely based on the posterior distributions and does not require any additional information from the data or the model (e.g., such as priors, as in the case of Bayes factors).
It is robust to the scale of both the response variable and the predictors.
It is strongly correlated with the frequentist p-value, and can thus be used to draw parallels and give some reference to readers non-familiar with Bayesian statistics (Makowski et al., 2019).
Relationship with the p-value
In most cases, it seems that the pd has a direct correspondence with the
frequentist one-sided p-value through the formula (for two-sided p):
p = 2 * (1 - pd)
Thus, a two-sided p-value of respectively .1, .05, .01 and .001 would
correspond approximately to a pd of 95%, 97.5%, 99.5% and 99.95%.
See pd_to_p() for details.
Possible Range of Values
The largest value pd can take is 1 - the posterior is strictly directional. However, the smallest value pd can take depends on the parameter space represented by the posterior.
For a continuous parameter space, exact values of 0 (or any point null
value) are not possible, and so 100% of the posterior has some sign, some
positive, some negative. Therefore, the smallest the pd can be is 0.5 -
with an equal posterior mass of positive and negative values. Values close to
0.5 cannot be used to support the null hypothesis (that the parameter does
not have a direction) is a similar why to how large p-values cannot be used
to support the null hypothesis (see pd_to_p(); Makowski et al., 2019).
For a discrete parameter space or a parameter space that is a mixture between discrete and continuous spaces, exact values of 0 (or any point null value) are possible! Therefore, the smallest the pd can be is 0 - with 100% of the posterior mass on 0. Thus values close to 0 can be used to support the null hypothesis (see van den Bergh et al., 2021).
Examples of posteriors representing discrete parameter space:
When a parameter can only take discrete values.
When a mixture prior/posterior is used (such as the spike-and-slab prior; see van den Bergh et al., 2021).
When conducting Bayesian model averaging (e.g.,
weighted_posteriors()orbrms::posterior_average).
Statistical inference - how to quantify evidence
There is no standardized approach to drawing conclusions based on the available data and statistical models. A frequently chosen but also much criticized approach is to evaluate results based on their statistical significance (Amrhein et al. 2017).
A more sophisticated way would be to test whether estimated effects exceed the "smallest effect size of interest", to avoid even the smallest effects being considered relevant simply because they are statistically significant, but clinically or practically irrelevant (Lakens et al. 2018, Lakens 2024).
A rather unconventional approach, which is nevertheless advocated by various authors, is to interpret results from classical regression models either in terms of probabilities, similar to the usual approach in Bayesian statistics (Schweder 2018; Schweder and Hjort 2003; Vos 2022) or in terms of relative measure of "evidence" or "compatibility" with the data (Greenland et al. 2022; Rafi and Greenland 2020), which nevertheless comes close to a probabilistic interpretation.
A more detailed discussion of this topic is found in the documentation of
p_function().
The parameters package provides several options or functions to aid statistical inference. These are, for example:
equivalence_test(), to compute the (conditional) equivalence test for frequentist modelsp_significance(), to compute the probability of practical significance, which can be conceptualized as a unidirectional equivalence testp_function(), or consonance function, to compute p-values and compatibility (confidence) intervals for statistical modelsthe
pdargument (settingpd = TRUE) inmodel_parameters()includes a column with the probability of direction, i.e. the probability that a parameter is strictly positive or negative. SeebayestestR::p_direction()for details. If plotting is desired, thep_direction()function can be used, together withplot().the
s_valueargument (settings_value = TRUE) inmodel_parameters()replaces the p-values with their related S-values (Rafi and Greenland 2020)finally, it is possible to generate distributions of model coefficients by generating bootstrap-samples (setting
bootstrap = TRUE) or simulating draws from model coefficients usingsimulate_model(). These samples can then be treated as "posterior samples" and used in many functions from the bayestestR package.
Most of the above shown options or functions derive from methods originally
implemented for Bayesian models (Makowski et al. 2019). However, assuming
that model assumptions are met (which means, the model fits well to the data,
the correct model is chosen that reflects the data generating process
(distributional model family) etc.), it seems appropriate to interpret
results from classical frequentist models in a "Bayesian way" (more details:
documentation in p_function()).
References
Amrhein, V., Korner-Nievergelt, F., and Roth, T. (2017). The earth is flat (p > 0.05): Significance thresholds and the crisis of unreplicable research. PeerJ, 5, e3544. doi:10.7717/peerj.3544
Greenland S, Rafi Z, Matthews R, Higgs M. To Aid Scientific Inference, Emphasize Unconditional Compatibility Descriptions of Statistics. (2022) https://arxiv.org/abs/1909.08583v7 (Accessed November 10, 2022)
Lakens, D. (2024). Improving Your Statistical Inferences (Version v1.5.1). Retrieved from https://lakens.github.io/statistical_inferences/. doi:10.5281/ZENODO.6409077
Lakens, D., Scheel, A. M., and Isager, P. M. (2018). Equivalence Testing for Psychological Research: A Tutorial. Advances in Methods and Practices in Psychological Science, 1(2), 259–269.
Makowski, D., Ben-Shachar, M. S., Chen, S. H. A., and Lüdecke, D. (2019). Indices of Effect Existence and Significance in the Bayesian Framework. Frontiers in Psychology, 10, 2767. doi:10.3389/fpsyg.2019.02767
Rafi Z, Greenland S. Semantic and cognitive tools to aid statistical science: replace confidence and significance by compatibility and surprise. BMC Medical Research Methodology (2020) 20:244.
Schweder T. Confidence is epistemic probability for empirical science. Journal of Statistical Planning and Inference (2018) 195:116–125. doi:10.1016/j.jspi.2017.09.016
Schweder T, Hjort NL. Frequentist analogues of priors and posteriors. In Stigum, B. (ed.), Econometrics and the Philosophy of Economics: Theory Data Confrontation in Economics, pp. 285-217. Princeton University Press, Princeton, NJ, 2003
Vos P, Holbert D. Frequentist statistical inference without repeated sampling. Synthese 200, 89 (2022). doi:10.1007/s11229-022-03560-x
See also
See also equivalence_test(), p_function() and
p_significance() for functions related to checking effect existence and
significance.
Examples
data(qol_cancer)
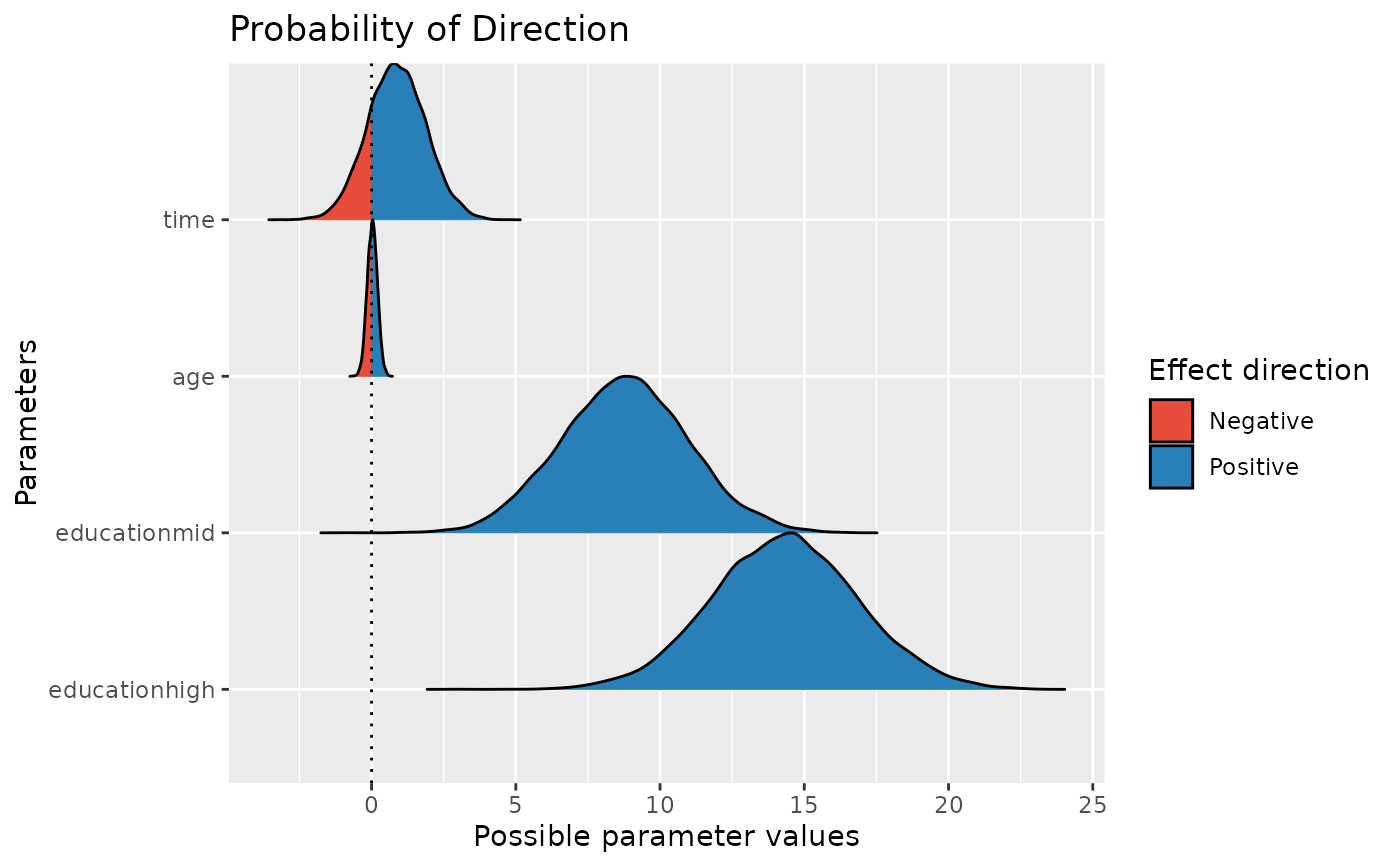
model <- lm(QoL ~ time + age + education, data = qol_cancer)
p_direction(model)
#> Probability of Direction (null: 0)
#>
#> Parameter | 95% CI | pd
#> ---------------------------------------
#> (Intercept) | [58.46, 69.28] | 100%
#> time | [-1.07, 2.85] | 81.47%
#> age | [-0.32, 0.37] | 55.91%
#> educationmid | [ 4.43, 13.09] | 99.99%
#> educationhigh | [ 9.33, 19.38] | 100%
# based on heteroscedasticity-robust standard errors
p_direction(model, vcov = "HC3")
#> Probability of Direction (null: 0)
#>
#> Parameter | 95% CI | pd
#> ---------------------------------------
#> (Intercept) | [58.33, 69.41] | 100%
#> time | [-1.13, 2.90] | 80.70%
#> age | [-0.33, 0.38] | 55.35%
#> educationmid | [ 4.21, 13.31] | 100%
#> educationhigh | [ 9.37, 19.34] | 100%
result <- p_direction(model)
plot(result)