Compute the (conditional) equivalence test for frequentist models.
Usage
# S3 method for class 'lm'
equivalence_test(
x,
range = "default",
ci = 0.95,
rule = "classic",
effects = "fixed",
vcov = NULL,
vcov_args = NULL,
verbose = TRUE,
...
)Arguments
- x
A statistical model.
- range
The range of practical equivalence of an effect. May be
"default", to automatically define this range based on properties of the model's data.- ci
Confidence Interval (CI) level. Default to
0.95(95%).- rule
Character, indicating the rules when testing for practical equivalence. Can be
"bayes","classic"or"cet". See 'Details'.- effects
Should parameters for fixed effects (
"fixed"), random effects ("random"), or both fixed and random effects ("all") be returned? By default, the variance components for random effects are returned. If group-level effects are requested,"grouplevel"returns the group-level random effects (BLUPs), while"random_total"return the overall (sum of fixed and random) effects (similar to whatcoef()returns). Using"grouplevel"is equivalent to settinggroup_level = TRUE. Theeffectsargument only applies to mixed models. If the calculation of random effects parameters takes too long, you may useeffects = "fixed".- vcov
Variance-covariance matrix used to compute uncertainty estimates (e.g., for robust standard errors). This argument accepts a covariance matrix, a function which returns a covariance matrix, or a string which identifies the function to be used to compute the covariance matrix.
A covariance matrix
A function which returns a covariance matrix (e.g.,
stats::vcov())A string which indicates the kind of uncertainty estimates to return.
Heteroskedasticity-consistent:
"HC","HC0","HC1","HC2","HC3","HC4","HC4m","HC5". See?sandwich::vcovHCCluster-robust:
"CR","CR0","CR1","CR1p","CR1S","CR2","CR3". See?clubSandwich::vcovCRBootstrap:
"BS","xy","residual","wild","mammen","fractional","jackknife","norm","webb". See?sandwich::vcovBSOther
sandwichpackage functions:"HAC","PC","CL","OPG","PL".
- vcov_args
List of arguments to be passed to the function identified by the
vcovargument. This function is typically supplied by the sandwich or clubSandwich packages. Please refer to their documentation (e.g.,?sandwich::vcovHAC) to see the list of available arguments. If no estimation type (argumenttype) is given, the default type for"HC"equals the default from the sandwich package; for type"CR", the default is set to"CR3".- verbose
Toggle warnings and messages.
- ...
Arguments passed to or from other methods.
Details
In classical null hypothesis significance testing (NHST) within a
frequentist framework, it is not possible to accept the null hypothesis, H0 -
unlike in Bayesian statistics, where such probability statements are
possible. "... one can only reject the null hypothesis if the test
statistics falls into the critical region(s), or fail to reject this
hypothesis. In the latter case, all we can say is that no significant effect
was observed, but one cannot conclude that the null hypothesis is true."
(Pernet 2017). One way to address this issues without Bayesian methods is
Equivalence Testing, as implemented in equivalence_test(). While you
either can reject the null hypothesis or claim an inconclusive result in
NHST, the equivalence test - according to Pernet - adds a third category,
"accept". Roughly speaking, the idea behind equivalence testing in a
frequentist framework is to check whether an estimate and its uncertainty
(i.e. confidence interval) falls within a region of "practical equivalence".
Depending on the rule for this test (see below), statistical significance
does not necessarily indicate whether the null hypothesis can be rejected or
not, i.e. the classical interpretation of the p-value may differ from the
results returned from the equivalence test.
Calculation of equivalence testing
"bayes" - Bayesian rule (Kruschke 2018)
This rule follows the "HDI+ROPE decision rule" (Kruschke, 2014, 2018) used for the
Bayesian counterpart(). This means, if the confidence intervals are completely outside the ROPE, the "null hypothesis" for this parameter is "rejected". If the ROPE completely covers the CI, the null hypothesis is accepted. Else, it's undecided whether to accept or reject the null hypothesis. Desirable results are low proportions inside the ROPE (the closer to zero the better)."classic" - The TOST rule (Lakens 2017)
This rule follows the "TOST rule", i.e. a two one-sided test procedure (Lakens 2017). Following this rule...
practical equivalence is assumed (i.e. H0 "accepted") when the narrow confidence intervals are completely inside the ROPE, no matter if the effect is statistically significant or not;
practical equivalence (i.e. H0) is rejected, when the coefficient is statistically significant, both when the narrow confidence intervals (i.e.
1-2*alpha) include or exclude the the ROPE boundaries, but the narrow confidence intervals are not fully covered by the ROPE;else the decision whether to accept or reject practical equivalence is undecided (i.e. when effects are not statistically significant and the narrow confidence intervals overlaps the ROPE).
"cet" - Conditional Equivalence Testing (Campbell/Gustafson 2018)
The Conditional Equivalence Testing as described by Campbell and Gustafson 2018. According to this rule, practical equivalence is rejected when the coefficient is statistically significant. When the effect is not significant and the narrow confidence intervals are completely inside the ROPE, we accept (i.e. assume) practical equivalence, else it is undecided.
Levels of Confidence Intervals used for Equivalence Testing
For rule = "classic", "narrow" confidence intervals are used for
equivalence testing. "Narrow" means, the the intervals is not 1 - alpha,
but 1 - 2 * alpha. Thus, if ci = .95, alpha is assumed to be 0.05
and internally a ci-level of 0.90 is used. rule = "cet" uses
both regular and narrow confidence intervals, while rule = "bayes"
only uses the regular intervals.
p-Values
The equivalence p-value is the area of the (cumulative) confidence distribution that is outside of the region of equivalence. It can be interpreted as p-value for rejecting the alternative hypothesis and accepting the "null hypothesis" (i.e. assuming practical equivalence). That is, a high p-value means we reject the assumption of practical equivalence and accept the alternative hypothesis.
Second Generation p-Value (SGPV)
Second generation p-values (SGPV) were proposed as a statistic that represents the proportion of data-supported hypotheses that are also null hypotheses (Blume et al. 2018, Lakens and Delacre 2020). It represents the proportion of the full confidence interval range (assuming a normally or t-distributed, equal-tailed interval, based on the model) that is inside the ROPE. The SGPV ranges from zero to one. Higher values indicate that the effect is more likely to be practically equivalent ("not of interest").
Note that the assumed interval, which is used to calculate the SGPV, is an estimation of the full interval based on the chosen confidence level. For example, if the 95% confidence interval of a coefficient ranges from -1 to 1, the underlying full (normally or t-distributed) interval approximately ranges from -1.9 to 1.9, see also following code:
# simulate full normal distribution
out <- bayestestR::distribution_normal(10000, 0, 0.5)
# range of "full" distribution
range(out)
# range of 95% CI
round(quantile(out, probs = c(0.025, 0.975)), 2)This ensures that the SGPV always refers to the general compatible parameter space of coefficients, independent from the confidence interval chosen for testing practical equivalence. Therefore, the SGPV of the full interval is similar to the ROPE coverage of Bayesian equivalence tests, see following code:
library(bayestestR)
library(brms)
m <- lm(mpg ~ gear + wt + cyl + hp, data = mtcars)
m2 <- brm(mpg ~ gear + wt + cyl + hp, data = mtcars)
# SGPV for frequentist models
equivalence_test(m)
# similar to ROPE coverage of Bayesian models
equivalence_test(m2)
# similar to ROPE coverage of simulated draws / bootstrap samples
equivalence_test(simulate_model(m))ROPE range
Some attention is required for finding suitable values for the ROPE limits
(argument range). See 'Details' in bayestestR::rope_range()
for further information.
Note
There is also a plot()-method
implemented in the see-package.
Statistical inference - how to quantify evidence
There is no standardized approach to drawing conclusions based on the available data and statistical models. A frequently chosen but also much criticized approach is to evaluate results based on their statistical significance (Amrhein et al. 2017).
A more sophisticated way would be to test whether estimated effects exceed the "smallest effect size of interest", to avoid even the smallest effects being considered relevant simply because they are statistically significant, but clinically or practically irrelevant (Lakens et al. 2018, Lakens 2024).
A rather unconventional approach, which is nevertheless advocated by various authors, is to interpret results from classical regression models either in terms of probabilities, similar to the usual approach in Bayesian statistics (Schweder 2018; Schweder and Hjort 2003; Vos 2022) or in terms of relative measure of "evidence" or "compatibility" with the data (Greenland et al. 2022; Rafi and Greenland 2020), which nevertheless comes close to a probabilistic interpretation.
A more detailed discussion of this topic is found in the documentation of
p_function().
The parameters package provides several options or functions to aid statistical inference. These are, for example:
equivalence_test(), to compute the (conditional) equivalence test for frequentist modelsp_significance(), to compute the probability of practical significance, which can be conceptualized as a unidirectional equivalence testp_function(), or consonance function, to compute p-values and compatibility (confidence) intervals for statistical modelsthe
pdargument (settingpd = TRUE) inmodel_parameters()includes a column with the probability of direction, i.e. the probability that a parameter is strictly positive or negative. SeebayestestR::p_direction()for details. If plotting is desired, thep_direction()function can be used, together withplot().the
s_valueargument (settings_value = TRUE) inmodel_parameters()replaces the p-values with their related S-values (Rafi and Greenland 2020)finally, it is possible to generate distributions of model coefficients by generating bootstrap-samples (setting
bootstrap = TRUE) or simulating draws from model coefficients usingsimulate_model(). These samples can then be treated as "posterior samples" and used in many functions from the bayestestR package.
Most of the above shown options or functions derive from methods originally
implemented for Bayesian models (Makowski et al. 2019). However, assuming
that model assumptions are met (which means, the model fits well to the data,
the correct model is chosen that reflects the data generating process
(distributional model family) etc.), it seems appropriate to interpret
results from classical frequentist models in a "Bayesian way" (more details:
documentation in p_function()).
References
Amrhein, V., Korner-Nievergelt, F., and Roth, T. (2017). The earth is flat (p > 0.05): Significance thresholds and the crisis of unreplicable research. PeerJ, 5, e3544. doi:10.7717/peerj.3544
Blume, J. D., D'Agostino McGowan, L., Dupont, W. D., & Greevy, R. A. (2018). Second-generation p-values: Improved rigor, reproducibility, & transparency in statistical analyses. PLOS ONE, 13(3), e0188299. https://doi.org/10.1371/journal.pone.0188299
Campbell, H., & Gustafson, P. (2018). Conditional equivalence testing: An alternative remedy for publication bias. PLOS ONE, 13(4), e0195145. doi: 10.1371/journal.pone.0195145
Greenland S, Rafi Z, Matthews R, Higgs M. To Aid Scientific Inference, Emphasize Unconditional Compatibility Descriptions of Statistics. (2022) https://arxiv.org/abs/1909.08583v7 (Accessed November 10, 2022)
Kruschke, J. K. (2014). Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press
Kruschke, J. K. (2018). Rejecting or accepting parameter values in Bayesian estimation. Advances in Methods and Practices in Psychological Science, 1(2), 270-280. doi: 10.1177/2515245918771304
Lakens, D. (2017). Equivalence Tests: A Practical Primer for t Tests, Correlations, and Meta-Analyses. Social Psychological and Personality Science, 8(4), 355–362. doi: 10.1177/1948550617697177
Lakens, D. (2024). Improving Your Statistical Inferences (Version v1.5.1). Retrieved from https://lakens.github.io/statistical_inferences/. doi:10.5281/ZENODO.6409077
Lakens, D., and Delacre, M. (2020). Equivalence Testing and the Second Generation P-Value. Meta-Psychology, 4. https://doi.org/10.15626/MP.2018.933
Lakens, D., Scheel, A. M., and Isager, P. M. (2018). Equivalence Testing for Psychological Research: A Tutorial. Advances in Methods and Practices in Psychological Science, 1(2), 259–269.
Makowski, D., Ben-Shachar, M. S., Chen, S. H. A., and Lüdecke, D. (2019). Indices of Effect Existence and Significance in the Bayesian Framework. Frontiers in Psychology, 10, 2767. doi:10.3389/fpsyg.2019.02767
Pernet, C. (2017). Null hypothesis significance testing: A guide to commonly misunderstood concepts and recommendations for good practice. F1000Research, 4, 621. doi: 10.12688/f1000research.6963.5
Rafi Z, Greenland S. Semantic and cognitive tools to aid statistical science: replace confidence and significance by compatibility and surprise. BMC Medical Research Methodology (2020) 20:244.
Schweder T. Confidence is epistemic probability for empirical science. Journal of Statistical Planning and Inference (2018) 195:116–125. doi:10.1016/j.jspi.2017.09.016
Schweder T, Hjort NL. Frequentist analogues of priors and posteriors. In Stigum, B. (ed.), Econometrics and the Philosophy of Economics: Theory Data Confrontation in Economics, pp. 285-217. Princeton University Press, Princeton, NJ, 2003
Vos P, Holbert D. Frequentist statistical inference without repeated sampling. Synthese 200, 89 (2022). doi:10.1007/s11229-022-03560-x
See also
For more details, see bayestestR::equivalence_test(). Further
readings can be found in the references. See also p_significance() for
a unidirectional equivalence test.
Examples
data(qol_cancer)
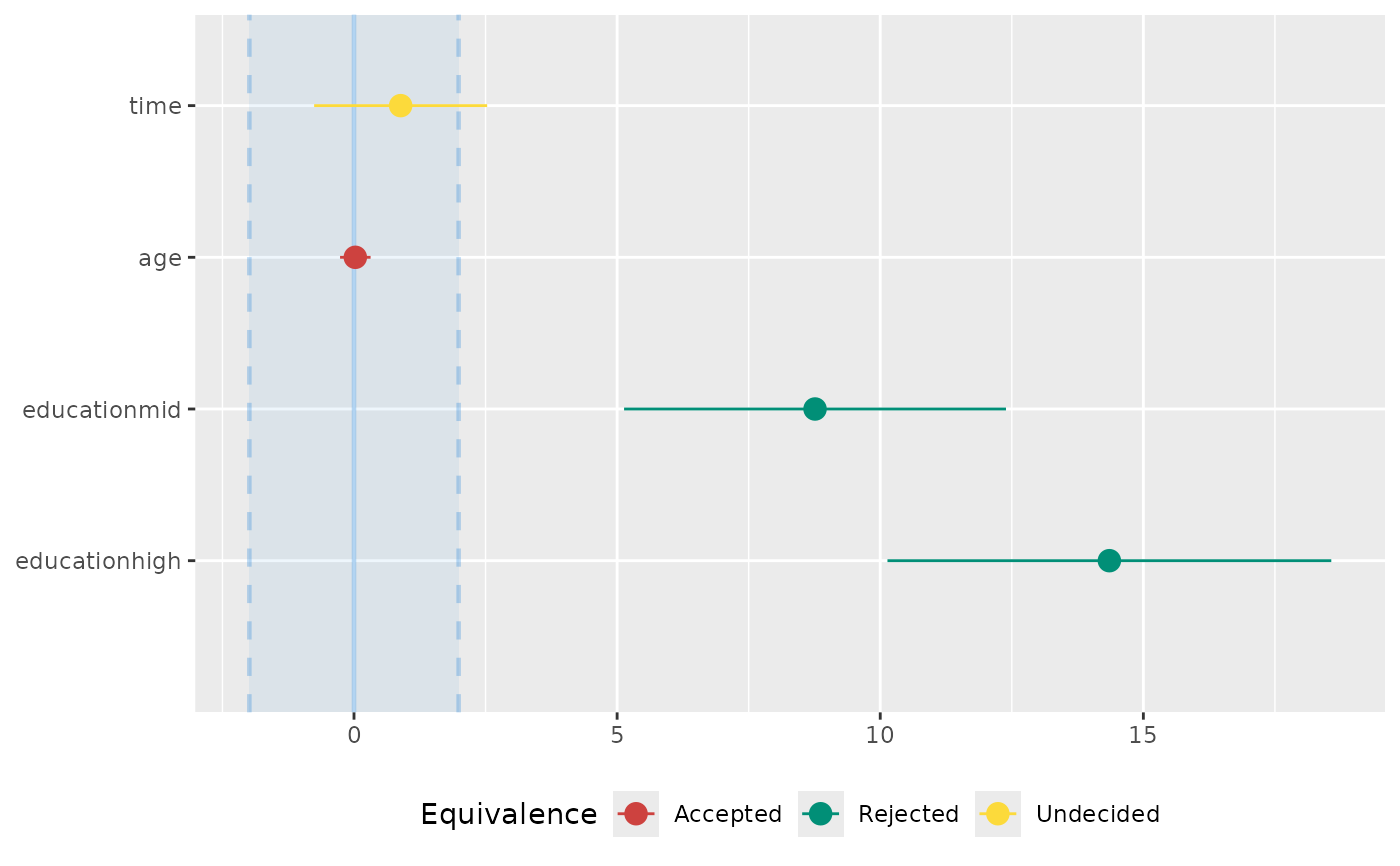
model <- lm(QoL ~ time + age + education, data = qol_cancer)
# default rule
equivalence_test(model)
#> # TOST-test for Practical Equivalence
#>
#> ROPE: [-1.99 1.99]
#>
#> Parameter | 90% CI | SGPV | Equivalence | p
#> -----------------------------------------------------------------
#> (Intercept) | [59.33, 68.41] | < .001 | Rejected | > .999
#> time | [-0.76, 2.53] | 0.905 | Undecided | 0.137
#> age | [-0.26, 0.32] | > .999 | Accepted | < .001
#> education [mid] | [ 5.13, 12.39] | < .001 | Rejected | 0.999
#> education [high] | [10.14, 18.57] | < .001 | Rejected | > .999
# using heteroscedasticity-robust standard errors
equivalence_test(model, vcov = "HC3")
#> # TOST-test for Practical Equivalence
#>
#> ROPE: [-1.99 1.99]
#>
#> Parameter | 90% CI | SGPV | Equivalence | p
#> -----------------------------------------------------------------
#> (Intercept) | [59.22, 68.52] | < .001 | Rejected | > .999
#> time | [-0.80, 2.57] | 0.899 | Undecided | 0.144
#> age | [-0.27, 0.32] | > .999 | Accepted | < .001
#> education [mid] | [ 4.95, 12.58] | < .001 | Rejected | 0.998
#> education [high] | [10.17, 18.54] | < .001 | Rejected | > .999
# conditional equivalence test
equivalence_test(model, rule = "cet")
#> # Conditional Equivalence Testing
#>
#> ROPE: [-1.99 1.99]
#>
#> Parameter | 90% CI | SGPV | Equivalence | p
#> -----------------------------------------------------------------
#> (Intercept) | [59.33, 68.41] | < .001 | Rejected | > .999
#> time | [-0.76, 2.53] | 0.905 | Undecided | 0.137
#> age | [-0.26, 0.32] | > .999 | Accepted | < .001
#> education [mid] | [ 5.13, 12.39] | < .001 | Rejected | 0.999
#> education [high] | [10.14, 18.57] | < .001 | Rejected | > .999
# plot method
if (require("see", quietly = TRUE)) {
result <- equivalence_test(model)
plot(result)
}