Simulate data with specific characteristics.
Usage
simulate_correlation(n = 100, r = 0.5, mean = 0, sd = 1, names = NULL, ...)
simulate_ttest(n = 100, d = 0.5, names = NULL, ...)
simulate_difference(n = 100, d = 0.5, names = NULL, ...)Arguments
- n
The number of observations to be generated.
- r
A value or vector corresponding to the desired correlation coefficients.
- mean
A value or vector corresponding to the mean of the variables.
- sd
A value or vector corresponding to the SD of the variables.
- names
A character vector of desired variable names.
- ...
Arguments passed to or from other methods.
- d
A value or vector corresponding to the desired difference between the groups.
Examples
# Correlation --------------------------------
data <- simulate_correlation(r = 0.5)
plot(data$V1, data$V2)
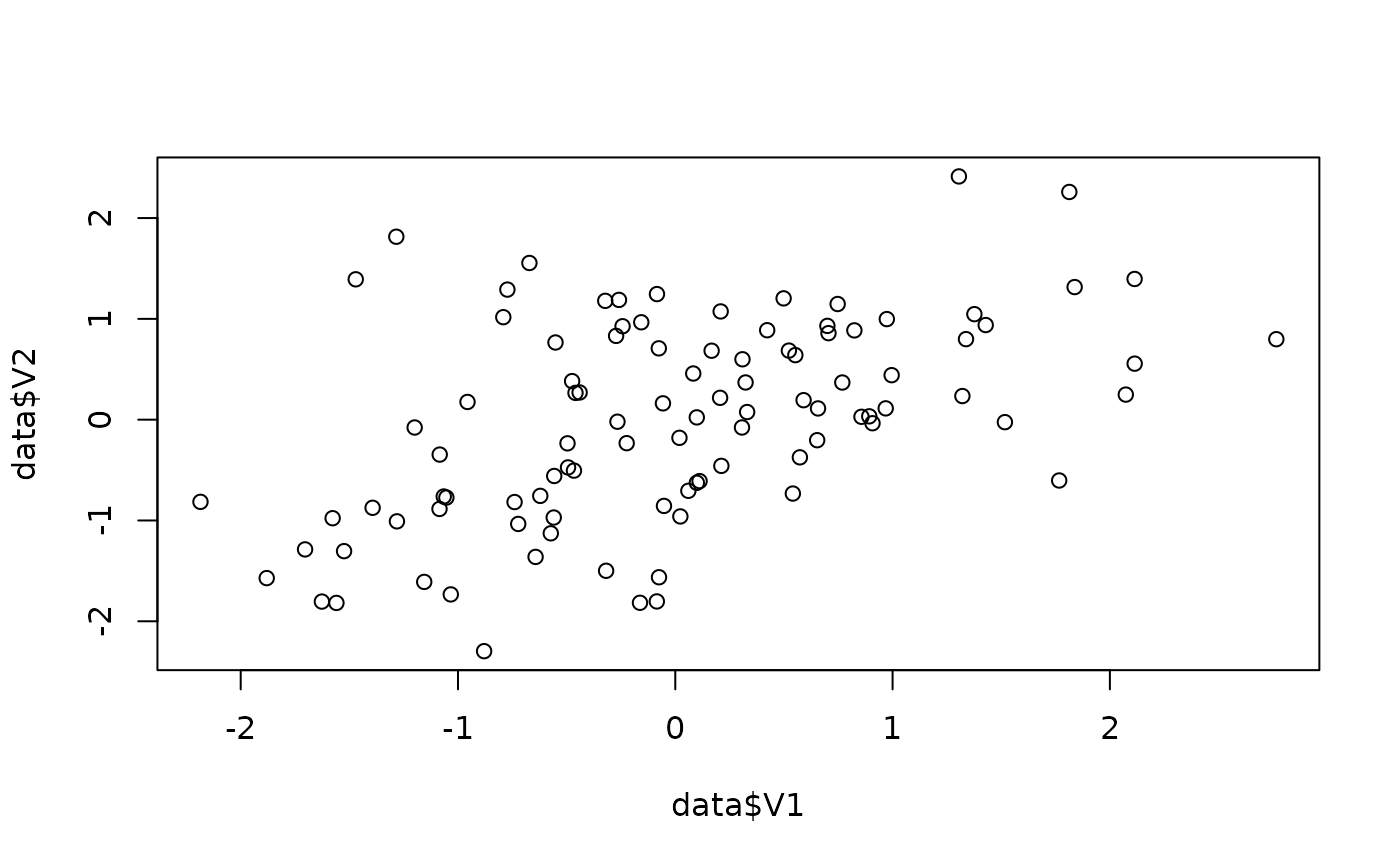cor.test(data$V1, data$V2)
#>
#> Pearson's product-moment correlation
#>
#> data: data$V1 and data$V2
#> t = 5.7155, df = 98, p-value = 1.18e-07
#> alternative hypothesis: true correlation is not equal to 0
#> 95 percent confidence interval:
#> 0.3366433 0.6341398
#> sample estimates:
#> cor
#> 0.5
#>
summary(lm(V2 ~ V1, data = data))
#>
#> Call:
#> lm(formula = V2 ~ V1, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.8766 -0.5691 -0.1028 0.5029 2.4303
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -5.201e-17 8.704e-02 0.000 1
#> V1 5.000e-01 8.748e-02 5.715 1.18e-07 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.8704 on 98 degrees of freedom
#> Multiple R-squared: 0.25, Adjusted R-squared: 0.2423
#> F-statistic: 32.67 on 1 and 98 DF, p-value: 1.18e-07
#>
# Specify mean and SD
data <- simulate_correlation(r = 0.5, n = 50, mean = c(0, 1), sd = c(0.7, 1.7))
cor.test(data$V1, data$V2)
#>
#> Pearson's product-moment correlation
#>
#> data: data$V1 and data$V2
#> t = 4, df = 48, p-value = 0.000218
#> alternative hypothesis: true correlation is not equal to 0
#> 95 percent confidence interval:
#> 0.2574879 0.6832563
#> sample estimates:
#> cor
#> 0.5
#>
round(c(mean(data$V1), sd(data$V1)), 1)
#> [1] 0.0 0.7
round(c(mean(data$V2), sd(data$V2)), 1)
#> [1] 1.0 1.7
summary(lm(V2 ~ V1, data = data))
#>
#> Call:
#> lm(formula = V2 ~ V1, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.5307 -0.9430 0.2124 0.7561 2.9882
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.0000 0.2104 4.754 1.86e-05 ***
#> V1 1.2143 0.3036 4.000 0.000218 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 1.487 on 48 degrees of freedom
#> Multiple R-squared: 0.25, Adjusted R-squared: 0.2344
#> F-statistic: 16 on 1 and 48 DF, p-value: 0.000218
#>
# Generate multiple variables
cor_matrix <- matrix(
c(
1.0, 0.2, 0.4,
0.2, 1.0, 0.3,
0.4, 0.3, 1.0
),
nrow = 3
)
data <- simulate_correlation(r = cor_matrix, names = c("y", "x1", "x2"))
cor(data)
#> y x1 x2
#> y 1.0 0.2 0.4
#> x1 0.2 1.0 0.3
#> x2 0.4 0.3 1.0
summary(lm(y ~ x1, data = data))
#>
#> Call:
#> lm(formula = y ~ x1, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.32830 -0.63976 0.03418 0.53242 2.58234
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -8.900e-18 9.848e-02 0.000 1.000
#> x1 2.000e-01 9.897e-02 2.021 0.046 *
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.9848 on 98 degrees of freedom
#> Multiple R-squared: 0.04, Adjusted R-squared: 0.0302
#> F-statistic: 4.083 on 1 and 98 DF, p-value: 0.04604
#>
# t-test --------------------------------
data <- simulate_ttest(n = 30, d = 0.3)
plot(data$V1, data$V0)
round(c(mean(data$V1), sd(data$V1)), 1)
#> [1] 0 1
diff(t.test(data$V1 ~ data$V0)$estimate)
#> mean in group 1
#> 0.08559378
summary(lm(V1 ~ V0, data = data))
#>
#> Call:
#> lm(formula = V1 ~ V0, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.09095 -0.63342 0.03709 0.66480 2.16514
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.03709 0.24557 -0.151 0.881
#> V01 0.08559 0.37305 0.229 0.820
#>
#> Residual standard error: 1.013 on 28 degrees of freedom
#> Multiple R-squared: 0.001877, Adjusted R-squared: -0.03377
#> F-statistic: 0.05265 on 1 and 28 DF, p-value: 0.8202
#>
summary(glm(V0 ~ V1, data = data, family = "binomial"))
#>
#> Call:
#> glm(formula = V0 ~ V1, family = "binomial", data = data)
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -0.26877 0.36881 -0.729 0.466
#> V1 0.08944 0.37724 0.237 0.813
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 41.054 on 29 degrees of freedom
#> Residual deviance: 40.998 on 28 degrees of freedom
#> AIC: 44.998
#>
#> Number of Fisher Scoring iterations: 4
#>
# Difference --------------------------------
data <- simulate_difference(n = 30, d = 0.3)
plot(data$V1, data$V0)
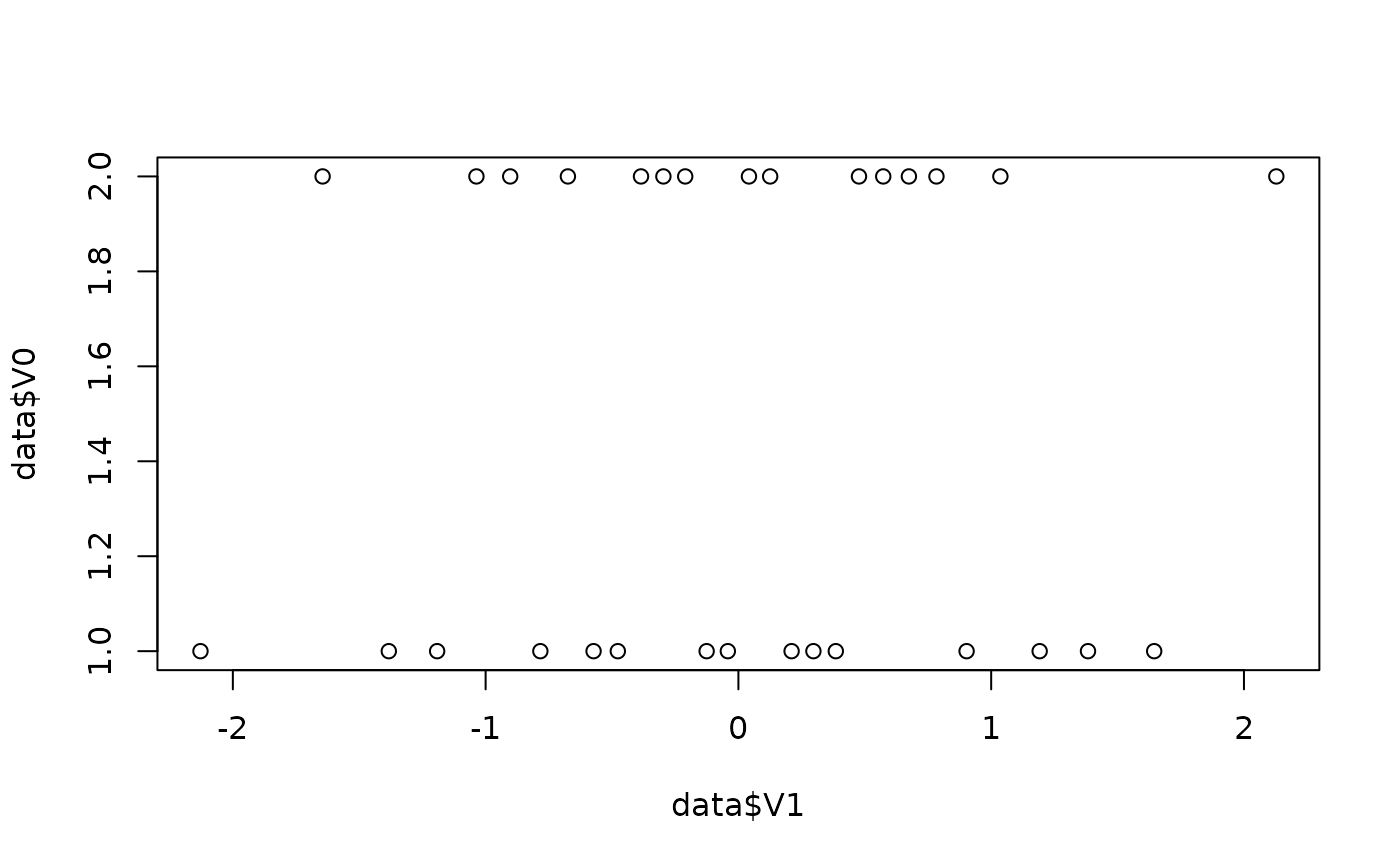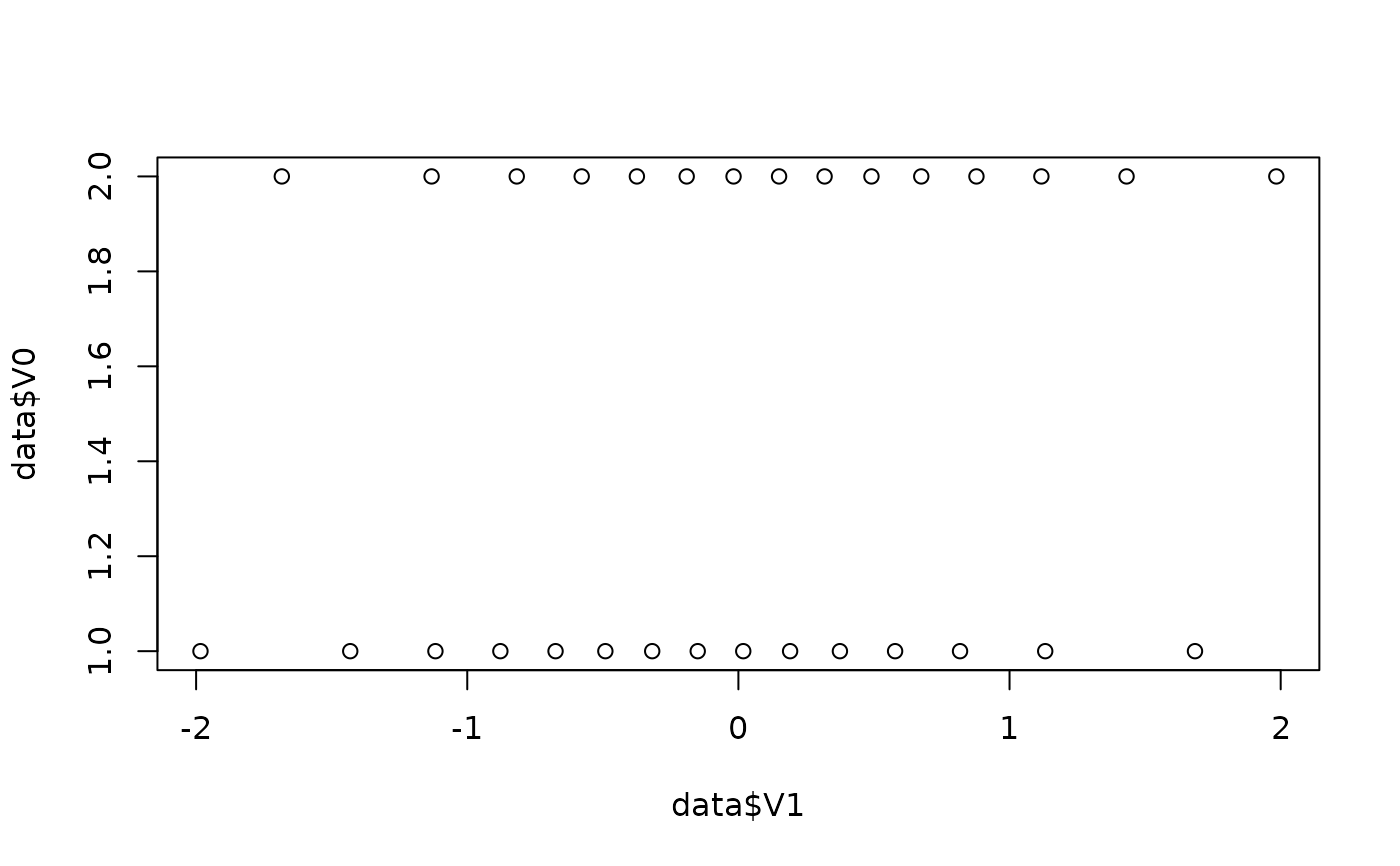round(c(mean(data$V1), sd(data$V1)), 1)
#> [1] 0 1
diff(t.test(data$V1 ~ data$V0)$estimate)
#> mean in group 1
#> 0.3
summary(lm(V1 ~ V0, data = data))
#>
#> Call:
#> lm(formula = V1 ~ V0, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.834 -0.677 0.000 0.677 1.834
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.1500 0.2562 -0.586 0.563
#> V01 0.3000 0.3623 0.828 0.415
#>
#> Residual standard error: 0.9922 on 28 degrees of freedom
#> Multiple R-squared: 0.0239, Adjusted R-squared: -0.01096
#> F-statistic: 0.6857 on 1 and 28 DF, p-value: 0.4146
#>
summary(glm(V0 ~ V1, data = data, family = "binomial"))
#>
#> Call:
#> glm(formula = V0 ~ V1, family = "binomial", data = data)
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -4.569e-17 3.696e-01 0.000 1.000
#> V1 3.251e-01 3.877e-01 0.839 0.402
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 41.589 on 29 degrees of freedom
#> Residual deviance: 40.865 on 28 degrees of freedom
#> AIC: 44.865
#>
#> Number of Fisher Scoring iterations: 4
#>