Check if a distribution is unimodal or multimodal — check

For univariate distributions (one-dimensional vectors), this functions performs a Ameijeiras-Alonso et al. (2018) excess mass test. For multivariate distributions (data frames), it uses mixture modelling. However, it seems that it always returns a significant result (suggesting that the distribution is multimodal). A better method might be needed here.

Usage

check_multimodal(x, ...)

Arguments

x: A numeric vector or a data frame.
...: Arguments passed to or from other methods.

References

Ameijeiras-Alonso, J., Crujeiras, R. M., and Rodríguez-Casal, A. (2019). Mode testing, critical bandwidth and excess mass. Test, 28(3), 900-919.

Examples

# \donttest{
# Univariate
x <- rnorm(1000)
check_multimodal(x)
#> # Is the variable multimodal?
#> 
#> The Ameijeiras-Alonso et al. (2018) excess mass test suggests that the
#>   hypothesis of a multimodal distribution cannot be rejected (excess mass
#>   = 0.02, p = 0.262).
#> 

x <- c(rnorm(1000), rnorm(1000, 2))
check_multimodal(x)
#> # Is the variable multimodal?
#> 
#> The Ameijeiras-Alonso et al. (2018) excess mass test suggests that the
#>   distribution is significantly multimodal (excess mass = 0.02, p =
#>   0.040).
#> 

# Multivariate
m <- data.frame(
  x = rnorm(200),
  y = rbeta(200, 2, 1)
)
plot(m$x, m$y)

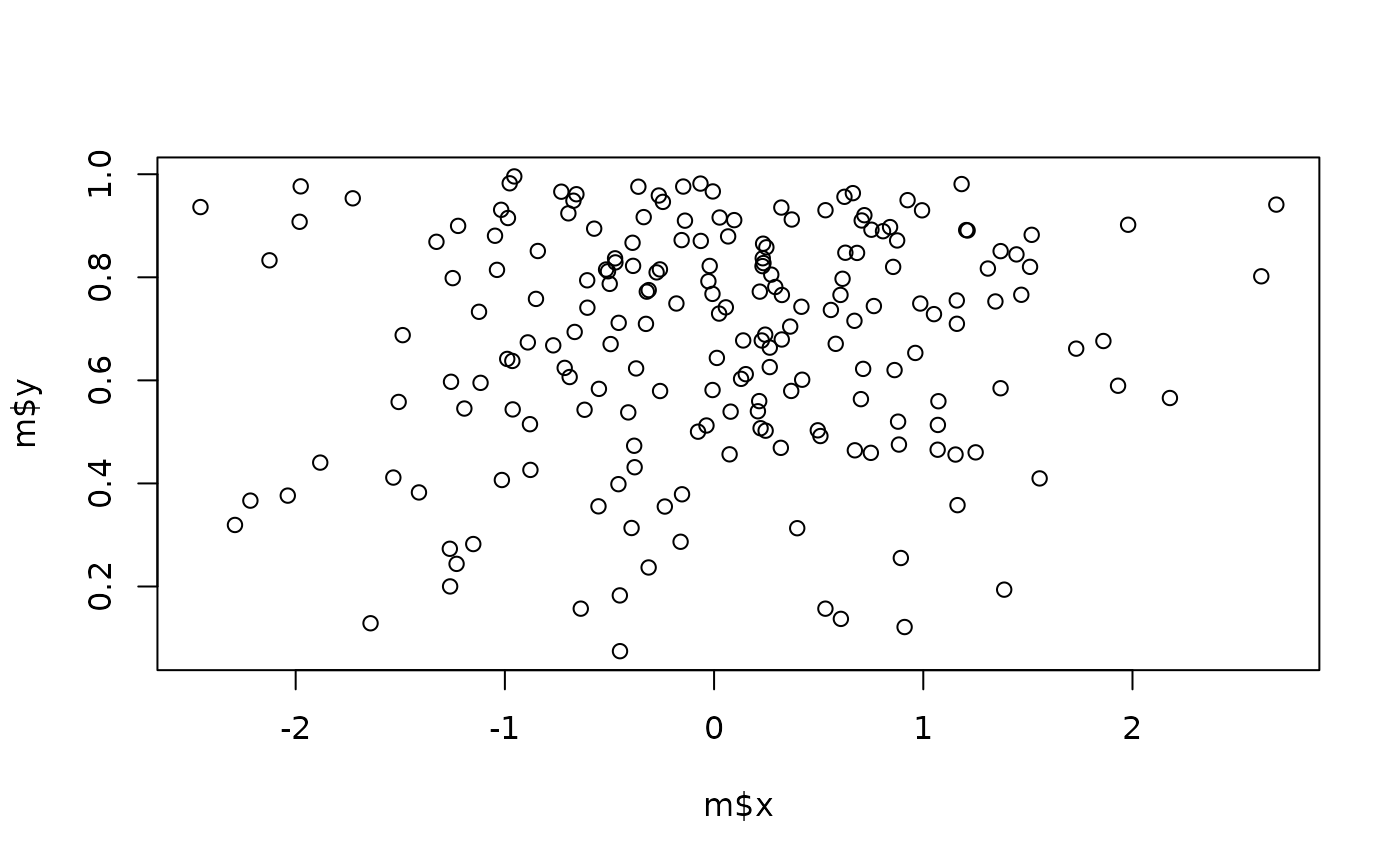check_multimodal(m)
#> # Is the data multimodal?
#> 
#> The parametric mixture modelling test suggests that the multivariate
#>   distribution is significantly multimodal (Chi2(8) = 25.13, p = 0.001).
#> 

m <- data.frame(
  x = c(rnorm(100), rnorm(100, 4)),
  y = c(rbeta(100, 2, 1), rbeta(100, 1, 4))
)
plot(m$x, m$y)

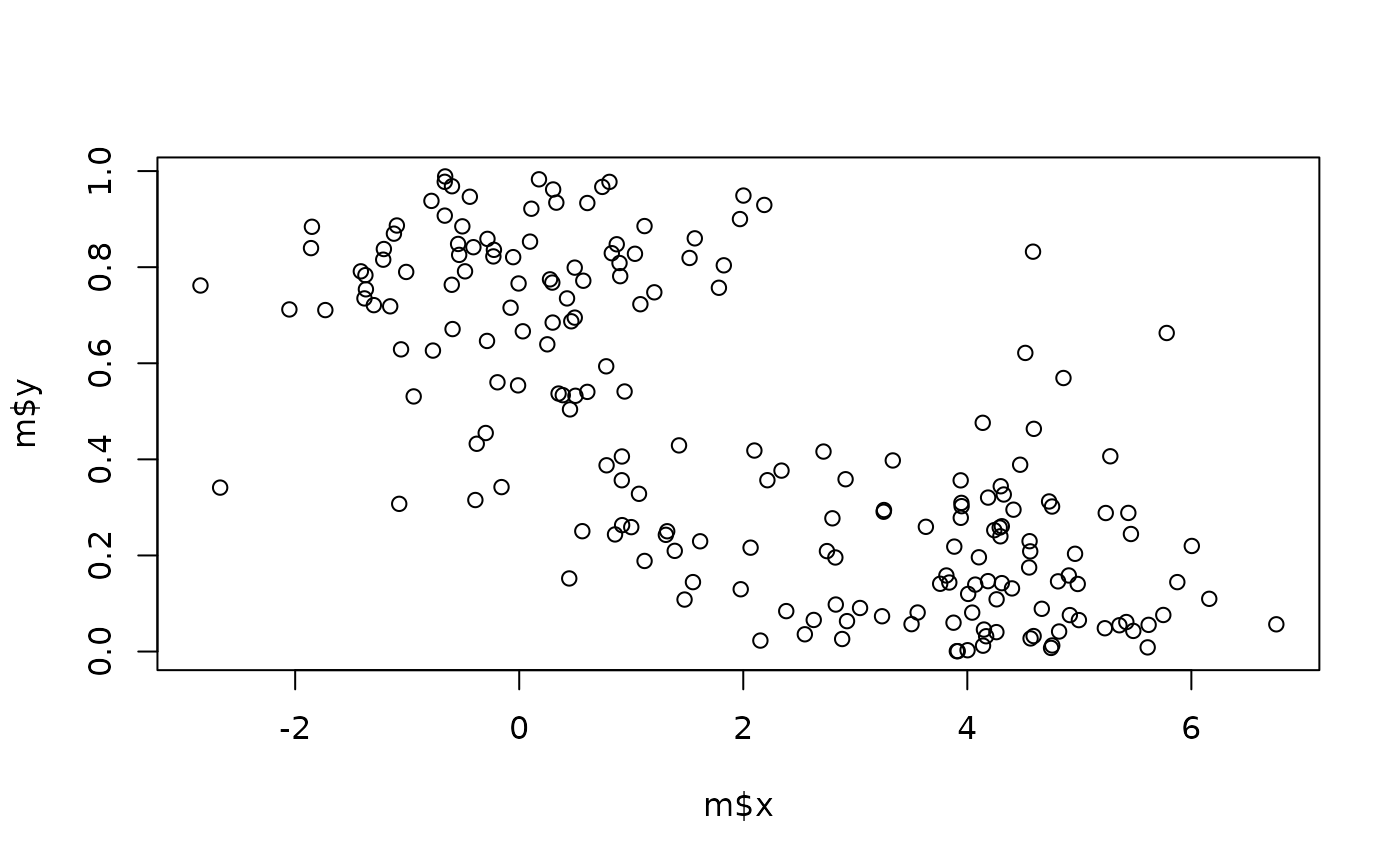check_multimodal(m)
#> # Is the data multimodal?
#> 
#> The parametric mixture modelling test suggests that the multivariate
#>   distribution is significantly multimodal (Chi2(11) = 78.42, p < .001).
#> 
# }