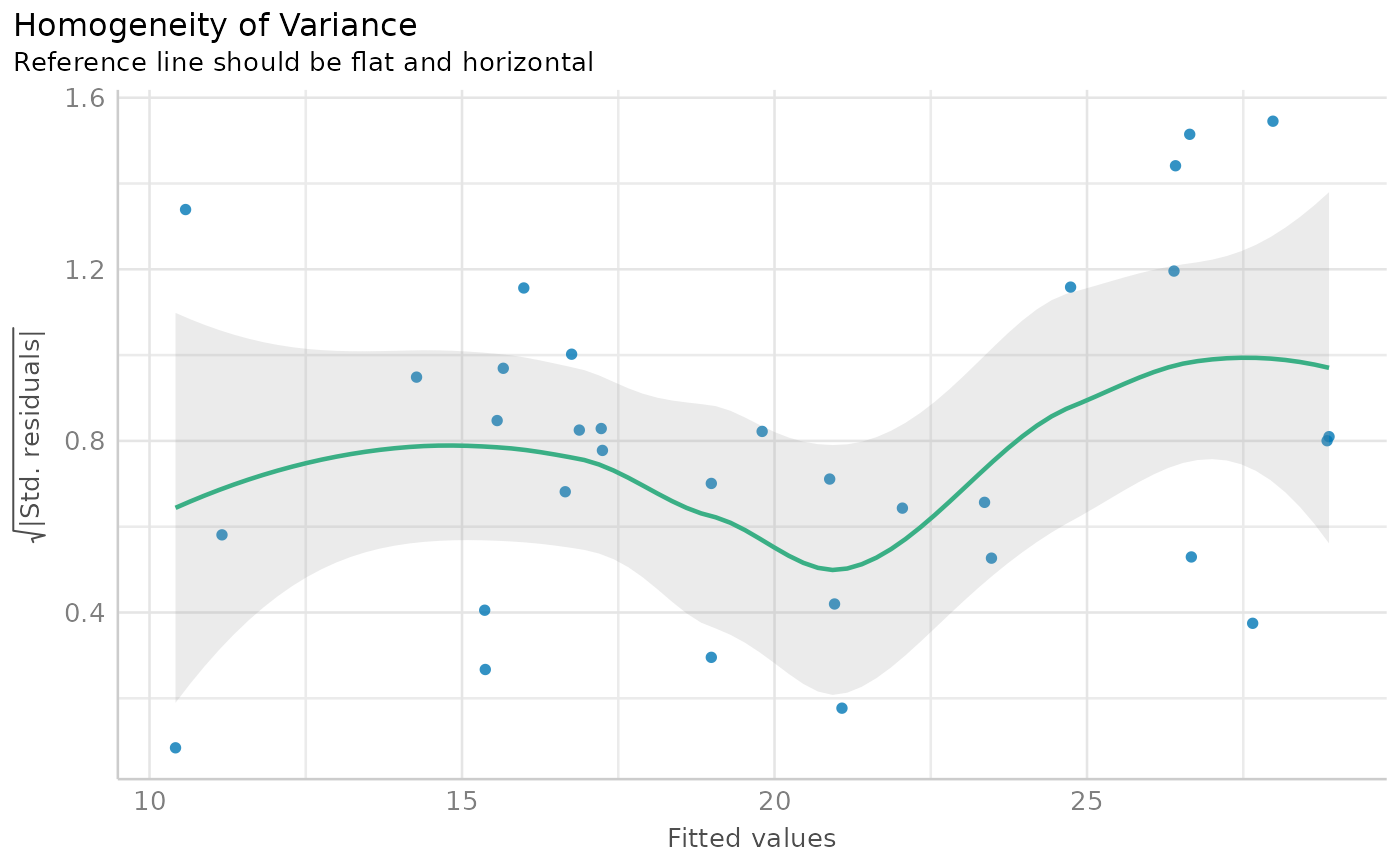
Check model for (non-)constant error variance

Significance testing for linear regression models assumes that the model errors (or residuals) have constant variance. If this assumption is violated the p-values from the model are no longer reliable.

Usage

check_heteroscedasticity(x, ...)

check_heteroskedasticity(x, ...)

Arguments

x

A model object.

...

Currently not used.

Value

The p-value of the test statistics. A p-value < 0.05 indicates a non-constant variance (heteroskedasticity).

Details

This test of the hypothesis of (non-)constant error is also called Breusch-Pagan test (1979).

Note

There is also a plot()-method implemented in the see-package.

References

Breusch, T. S., and Pagan, A. R. (1979) A simple test for heteroscedasticity and random coefficient variation. Econometrica 47, 1287-1294.

See also

Other functions to check model assumptions and and assess model quality: check_autocorrelation(), check_collinearity(), check_convergence(), check_homogeneity(), check_model(), check_outliers(), check_overdispersion(), check_predictions(), check_singularity(), check_zeroinflation()

Examples

m <<- lm(mpg ~ wt + cyl + gear + disp, data = mtcars)
check_heteroscedasticity(m)
#> Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.042).
#> 

# plot results
x <- check_heteroscedasticity(m)
plot(x)